Project Ideas
These are ideas for projects for GEC/Path Academics students.
Music Perception
These projects are inspired by Music, Cognition, and Computerized
Sound, edited by Perry R. Cook.
Shepard Tones
Shepard tones are tones with harmonics that are all an octave apart,
as shown here (from Michael Bach's
website):
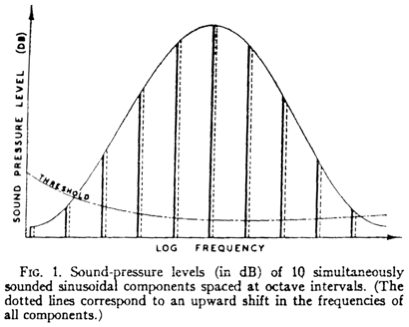 A curious property of Shepard Tones is they have no definite absolute
pitch: If you transpose everything up one octave, you get the same
spectrum. One famous effect is continuously sweeping Shepard Tones
upward. This can go on for octaves and yet the pitch is no
“higher” at the end than when it began.
A curious property of Shepard Tones is they have no definite absolute
pitch: If you transpose everything up one octave, you get the same
spectrum. One famous effect is continuously sweeping Shepard Tones
upward. This can go on for octaves and yet the pitch is no
“higher” at the end than when it began.
Nyquist has an implementation of Shepard Tones (look for Shepard in
the Nyquist Extensions list you can get from a menu in the NyquistIDE).
What can you do with this idea?
Shepard Tones from Conventional Tones
You could get an approximation of Shepard Tones by playing all octaves
of a given pitch class with any synthesizer. E.g. instead of C4, play
a combination of C1, C2, C3, C4, C5, C6, C7, C8. Does this work? Do
some sounds work better than others? E.g. piano vs. violin? Does
vibrato increase or decrease the perceived effect? Do bright tones or
dull tones increase or decrease the perceived effect? What about
filtering the tones to diminish the intensity of harmonics, making
them more sinusoidal as in true Shepard Tones? Are these sounds
beautiful? Ignoring the effect, what sounds are the most interesting
musically and esthetically?
Shepard Tones in Music Compositions
With Shepard Tones, you can melodies or harmonies that continuously
increase or decrease in pitch (or so it seems),
such as simple scales that go up forever, a chord progression that
follows the circle of fifths downward (or ii-V7-I, transpose down a
major second and do it again, repeat forever; e.g. dm, G7, Cmaj, Cmin,
F7, Bbmaj, bbmin, Eb7, Abmaj, ...). What interesting music can you
create this way?
Shifting Pitch
The image above shows the loudest partial at some unspecified middle
frequency. By shifting the “envelope” describing
amplitude, you can make the overall Tone sound higher or lower in
pitch. Thus you can make the sense of pitch go up and down
independently from changes in pitch class. E.g. the pitch class can go
from C to D (up) while the spectral envelope goes down. You could make
interesting sequences of Shepard Tones or extend the “Shepard
Tones from Conventional Tones“ in this way.
“Holy” Spectra
When we hear sound, our ears separate the spectrum into so-called
“critical bands.” We hear beating when there is more than
one sinusoidal component within the same band. Critical bands become
wider in frequency at higher frequencies, while the harmonic series
has constant spacing of harmonics, so at higher harmonic numbers,
multiple harmonics fall into the same critical band. Max Mathes and
John Pierce invented “Holy” spectra, where they remove
harmonics that would fall into the same critical band, and they claim
this allows sounds to be bright (lots of high frequency energy)
without sounding so “buzzy.”
Implement Holy Spectra using additive synthesis in Nyquist. Compare
the quality of Holy Spectra to tones with the samed perceived loudness
but with all harmonics.
Perceptual Fusion
John Chowning created some fascinating sounds by synthesizing 3-note chords
using additive synthesis with perfectly steady sinusoidal
harmonics. When presented with a collection of sinusoids, the ear does
not immediately group them into 3 tones. The effect can be intensified
by giving all the tones an exponential decay (creating a
bell-like sound) or introducing the partials in some random sequence
(as if they each come from a separate source). After some time when
the ear fails to make sense of all this (or perceives something other
than 3 tones), Chowning adds vibrato to the 3 tones. Each of the 3
sets of partials gets their own vibrato or random variation. Soon, the
ear concludes that the best interpretation of the partials is to fuse
the partials of each tone into a single tone, and the human perception
“flips” to hearing a 3-note chord.
Recreate This Effect
Use this technique to create some similar sonic illusions. Once the 3
tones become a chord, can you then alter the vibrato in ways to cause
other groupings or to group all partials together again?
Highlighting Partials
It follows that if within a tone you pick one partial and add
some vibrato, the partial might separate perceptually and allow you to
actually hear the individual partial.
This might be interesting to demonstrate how tones consist of a
harmonic series. Can you make a tone and as the tone plays, highlight
each partial in sequence by using vibrato?
It seems possible that you could also add vibrato to a set of
harmonic partials. In particular, harmonics 2, 4, 6, 8, ... should
sound an octave higher than the original tone. Can you split a tone
into even/odd partials in this way to produce two tones an octave apart?
Passive Nonlinearities
John Pierce suggests that in real acoustics, there are non-linearities
that give richness to sounds. Non-linearities can introduce energy
into a system and can be hard to control. Pierce describes
energy-conserving non-linearities as passive. One simple way to
obtain passive non-linearity is to model the system as a mass-spring
system where the spring constant is different depending one whether
the spring is stretched or compressed.
Model a string as set of 20 to 50 masses connected by springs. For
simplicity, allow the masses to move only in the transverse direction
(perpendicular to the length of the string). At one
end, give the mass a restoring force that is -A times the displacement
when the mass moves in one direction from rest, and -B times the
displacement when the mass moves in the other direction (for different
values of A and B). Synthesize tones and see what effects you can
obtain by varying A and B.
Synthesis Explorations
There are endless ways to create new sounds, and just as important as
creating a single sound is creating a method of
producing a whole class of sounds, analogous to inventing an
instrument. The control strategies are as important as the
sound because they give musicians control to shape their work
and not simply pick and choose from limited offerings.
Waveform Variation
Interesting sounds can be made by a sequence of waveforms that are
nearly identical from one period to the next but which change slowly
over time. One way to synthesize something like this (although
somewhat slow) is to make an array of samples of some fixed length,
covert them to a sound, and splice these single-period sounds
together, e.g. using SEQREP in Nyquist.
The results will have an integer number of samples per period,
which is a limitation, but it might be simpler to construct a sound
first close to the desired frequency and then resample (RESAMPLE in
Nyquist) to get an exact frequency if you need it.
PWL Breakpoint Modulation
One way to construct slowly varying waveforms is with a piece-wise
linear function (e.g. PWL in Nyquist), treating the breakpoint
coordinates as functions of time. E.g. they could modulate
sinusoidally at different slow rates (maybe 0.1 to 10 Hz), with some
care to avoid specifying breakpoints out of time order. What
interesting sounds can you construct?
Spline Interpolation
One problem with piece-wise linear functions is that angular
breakpoints do not occur in ordinary acoustic sounds and might result
in a busy or distorted sound, including some added aliasing
frequencies. Another approach might be using spline curves to produce
smoother waveforms. You can adapt spline equations to get continuity
between the end of one waveform and the beginning of the next. There
are many different types of splines to experiment with. You can use
various modulation techniques to move the spline control points slowly
compared to the frequency so that you get quasi-periodic sounds. What
interesting sounds can you construct with splines?
Deep Learning and Embeddings
Another approach to waveform control is to train a neural network to
encode waveforms. Using an auto-encoder, you can learn a mapping from a
low-dimensional space to a high-dimensional waveform, e.g. a 512-point
wavetable could be generated from a 5-dimensional hidden
layer. VQ-VAE is a refinement of auto-encoders that might be even
better. The system could be trained on a set of 512-point waveforms
from various sources.
Once trained, picking random points in the low-dimensional space
and interpolating between them should produce slowly varying waveforms
that can be appended and possibly frequency shifted using RESAMPLE to
make interesting tones.
One problem is likely to be that the system may not produce
waveforms that smoothly transition from the end back to the
beginning. If there is a discontinuity, or even a continuous but not
smooth curve, it will create high harmonics and might sound buzzy. One
way to deal with this is to work with spectra rather than time-domain
waveforms. If you represent only the harmonic amplitudes that vary
slowly, and if you synthesize the harmonics with the same phase in
every waveform (e.g. just use sines that are all zero at the
beginning of the waveform) then you will be guaranteed to actually get
that spectrum in the final signal.
Brass Models
There is a very
interesting
synthesis approach here in which some of the key elements of brass
(trumpet) oscillation and sound propagation are modeled, but without
any attempt to perform an accurate model lf the physics. While the
web page describes the model in terms of analog synthesizer modules,
this could all be implemented digitally. There are interesting
sound examples you can listen to on the webpage. Can you reproduce
this work? Can you create a nice library or instrument for Nyquist?
The section on “TRUMPET MODEL“ is part of a series
of pages on Acoustic Modelling. There are many ideas here that
could be implemented. Any of the pages would be a good starting
point for an interesting project to implement the technique in
Nyquist, produce some nice sound examples or a compoosition, and
package the example in an instrument to share with other Nyquist users.
VOSIM Synthesis
VOSIM is an interesting synthesis techniques with only a small number
of control parameters. It can produce interesting voice-like sounds
and sounds that seem to have strong resonances. Experiment with VOSIM
(look for a VOSIM implementation in Nyquist extensions) and develop
some compelling sounds.
Vibrato
Obtain recordings of singers and string instruments. Isolate some
nice-sounding notes where you hear vibrato. Use YIN (in
Nyquist) to estimate the frequency and RMS (in Nyquist) to estimate
amplitude variations. Use these to synthesize a tone, e.g. make a nice
tone with FMOSC or a table-lookup oscillator. Can you create a model
for vibrato that mimics the observations? Notice that there will be
some random fluctuations in pitch as well as sinusoidal variations and
even the sinusoidal variations will change in depth and
frequency. Nyquist's NOISE function can be used to make at randomness,
e.g. FORCE-SRATE(*DEFAULT-CONTROL-SRATE*, SOUND-SRATE-ABS(5, NOISE()))
~ DURATION will create a control-rate sound that smoothly changes
between random values placed every 1/5 second. The values range from 0
to 1.
- Applying only frequency vibrato to the synthesized tone, does
the result sound musical and natural?
- What about amplitude vibrato?
- What about both frequency and amplitude vibrato?
- If you are able to create a model that makes synthetic vibrato,
how does the model compare to the extracted data when applied to a
l synthetic tone?
- If the model works, listen to the synthesized tone with
variations of the model: frequency vibrato only, frequency vibrato
with no RANDON signal added, amplitude vibrato only, amplitude
vibrato without any RANDOM signal. Frequency and amplitude vibrato
without any RANDOM signals.
- There may be interesting parameters you can adjust in your
vibrato model, e.g. making vibrato deeper, faster, more random,
etc. Does anything sound better than the orignal data or the
unmodified model control?
Composition
There are many approaches to algorithmic composition. Here are some
suggested directions to pursue.
Fractals
See
Speech
Speech is a great source of material for music. There are many ways to
extract parameters to control algorithmic composition:
Amplitude Contour
In Nyquist, RMS can extract an amplitude envelope from any sound,
including speech. Speech phrases can become musical phrases. A classic
work exploiting this idea is Smalltalk by
Paul Lansky.
Pitch Contour
Similarly, you can extract pitch estimates with YIN in Nyquist. Note
that much of a speech signal will be consonants and space between
words where no pitch is well defined. YIN returns an aperiodicity
estimate on one channel. Only very low aperiodicity values are likely
to be correct pitches, so you need to filter the results of YIN, but
the resulting pitches can become the basis for melodies. You can
stretch the scale if the voice does not have the desired pitch range,
you can quantize pitches to scales of different kinds, etc.
Rhythm and Speech
By searching for peaks in the RMS (or possibly in the RMS derivative,
e.g. see Nyquist's SLOPE function), you can find interesting points of
articulation such as the beginnings of words or accents. You can then
split the speech audio into segments based on these articulation
points and reassemble the speech rhythmically, e.g. one segment every
250 ms, or quantize the speech timing to a rhythmic grid (e.g. shift
in time to the nearest multiple of 250 ms). Some interesting results
can be obtained.
Images
Images provide another interesting source of data. Here are some
possible ways to to incorporate image data into music making:
Pixel Processing
Extract either grayscale or RGB pixel values from an image to a text
file. E.g. the netpbm library has convenient command line tools, or
you can use Python and/or NumPy libraries to write pixel data to a
file. Once you have a text file with (long) lists of pixels, you can
use Nyquist's OPEN function to open the file and READ to read numbers.
One you have data in Nyquist, you can try many mappings. Here is an
example: Start with an image or image region that changes slowly from
one scan line to the next, but where there is some difference from
column to column, e.g. some vertical lines or edges. (An occasional
big change is probably good
too.) To make music, treat each scan line as a measure. E.g. just map
the pixel values in 8 columns to 8 pitches in a sequence of eighth
notes. Since the image changes slowly from scan line to scan line, the
measures will repeat, but if the image changes, there will be changes
in that measure. If there's a big change, e.g. scanning from the sky
to the horizon in a landscape, there will be a big sudden change.
There are infinite variations, e.g. you can use edge detection to
determine rhythms, or you can change the rhythm and the columns you
sample from every 8 measures or so.
Spectral Processing
Similar to the pixel processing above, you can map pixel values to the
amplitudes of harmonics. I recommend using pixels to construct PWL
functions that change smoothly since otherwise, noise in the image
could produce noisy results. Then simply control each sinusoidal
harmonic with a different PWL. An example of this (done in real-time
with live camera input) can be seen here. Notice how the water
waves scanning across the image produce spectral effects scanning
across frequency. Your results are of course sensitive to the choice
of video as well as your choice of mapping algorithm.
More Ideas
The slides from Week 5 contain more ideas.

